Tu dois devenir capable de
 |
Savoir
- Expliquer l'intérêt de l'usage
des outils abordés dans ce chapitre ;
- Citer les caractéristiques des différents éléments qui interviennent
dans le calcul d'une valeur cible ;
Savoir faire
- Utiliser l'outil « valeur cible » ;
- Utiliser
l'outil « solveur » en posant les
contraintes nécessaires ;
|
|
Atteindre une valeur cible
|
Les calculs effectués habituellement avec Excel utilisent
des valeurs numériques qui constituent les données d'un problème.
A l'aide d'un certain nombre de formules disposées dans les cellules
des feuilles de calculs, on détermine alors un ou plusieurs résultats.
Mais imaginons que, dans certains cas, on connaisse les résultats
attendus et que l'on se demande quelles doivent être les données.
- Donc, dans le
premier cas, c'est un peu comme si je calculais le prix à payer
pour acheter des barres de chocolat ; dans le deuxième cas,
je détermine combien de barres de chocolat je puis acheter avec
la somme dont je dispose.
- C'est tout
à fait cela. Mais attention à la crise de foie.
|
 |
En marche avant
 L'exemple très simple ci-contre permet d'illustrer
le concept :
- dans la cellule A2, indique la valeur 2
- dans la cellule B2, indique la valeur 7
- dans la cellule C2, indique la formule « =A2*B2 »
Le résultat de l'opération apparaît en C2. C'est bien 14.
|
|
En marche arrière
Posons-nous maintenant la question inverse.
Quelle devrait être la valeur de la cellule A2 pour obtenir
le résultat 28 dans la cellule C2?
On connaît le résultat calculé (28) , la
formule pour le calculer (=A2*B2), mais pas la première donnée.
L'animation ci-dessous indique la marche à suivre pour
faire déterminer quelle donnée fournira la résultat
attendu. Examine-la attentivement.
|
 |
Reproduis cette résolution en suivant les étapes indiquées ci-dessous.
- Dans une nouvelle feuille de calcul, indique les valeurs de A2,
B2 et la formule dans la cellule C2.
- Dans le menu Outils, sélectionne la commande Valeur cible
- Dans la boîte de dialogue Valeur cible, indique la référence
de la cellule dont tu souhaites définir la valeur. Dans le cas
présent, c'est la cellule C2. Clique sur le bouton
 et
désigne la cellule C2 par un clic de souris.
- Pour terminer, clique sur le bouton
 de
la boîte de dialogue Cellule à définir.
- Dans la zone de saisie Valeur à atteindre, indique
la valeur
28.
- Finalement, indique que la cellule à modifier est bien A2 par
la même méthode que tu as utilisée pour désigner C2.
- Clique sur OK.
Très rapidement, le tableur signale qu'il a trouvé une
solution possible avec la valeur 28 pour valeur cible.
|
|
Dans certains cas, il est possible que le tableur ne puisse
trouver de solution ou pas de solution exacte. Dans ce cas, les
informations données dans la boîte de dialogue
indiquent l'état de la résolution du problème
au moment de l'échec.
Les exemples ci-dessous correspondent à un autre calcul!
Le tableur trouve une solution
approximative |
Le tableur ne peut trouver
de solution |
|
|
|
|
A retenir!
Dans la recherche d'une valeur cible:
- la valeur ciblée doit se trouver dans une cellule
qui contient une formule
- la valeur ciblée doit obligatoirement être
un nombre
- la cellule à modifier ne peut contenir une formule
mais uniquement une valeur
|
|
|
| Quand tu te sens prêt(e) à répondre à quelques questions
sur les notions abordées ici, passe à l'étape suivante. |
Valeur cible: synthèse
|
| Quand tu as répondu à toutes les questions et bien compris
toutes les réponses, passe à l'étape suivante. |
Nombre de mensualités d'un emprunt
|
Tu es employé(e) de banque. Un client disposant d'un
certaine économie mensuelle
souhaite faire un emprunt. Il te demande de calculer combien de mensualités il
devra payer afin de rembourser cet emprunt, sans dépasser ses capacités
de remboursement.
Imaginons que le montant de l'emprunt soit de 5000 et que
les intérêts se montent à 0,35% par mois. Ce client peut disposer
de 200 d'économies par mois.
|
|
En marche avant
 Commençons par établir le calcul du montant du remboursement mensuel
dans les conditions précisées et pour 18 mois, par exemple.
- Etablis les titres dans la colonne A d'une feuille de calculs
vierge, comme dans l'illustration ci-contre.
- Dans la cellule B1, indique le montant de l'emprunt: soit 5 000 .
- Dans la cellule B2, indique la valeur du taux d'intérêt: soit
0,35%
- Dans la cellule B3, établis la formule qui permet
de calculer le montant des intérêts mensuels.
Quand tu as déterminé cette formule, écris-la.
Remarque que cette formule fonctionne pour n'importe quel montant
emprunté et pour n'importe quel taux.
- Dans la cellule B5, indique le nombre de mensualités envisagées.
- Dans la cellule B6, indique la formule qui calcule le montant
des intérêts pour le nombre de mensualités.
- Dans la cellule B7, indique la formule qui calcule le
montant total à payer, capital et intérêts.
- Dans la cellule B8, indique la formule qui calcule le
montant du remboursement mensuel.
Vérifie que les calculs sont corrects pour n'importe quel montant
emprunté et n'importe quel taux d'intérêt.
|
|
En marche arrière
Imaginons que notre client ne soit pas capable de rembourser 295,28 /mois,
comme dans l'exemple précédent. Combien de mensualités doit-il envisager
pour une capacité de remboursement mensuel de 200 ?
Quelle est ici la valeur cible? Quelle est la cellule variable?
Réponds à ces deux questions avant de poursuivre.
|
|
- Dans le menu Outils, sélectionne la commande Valeur
cible
- Dans la boîte de dialogue Valeur cible, indique
la référence de la cellule B8 comme cellule à définir.
- Indique la valeur 200 () pour valeur de cette cellule.
- Indique la cellule B5 comme cellule variable.
- Clique sur le bouton OK.
Le tableur détermine que le nombre de mensualités est 27,397.
- 27,397 mensualités?
Mais ça ne veut rien dire...
- Effectivement,
cela ne veut rien dire. Mais c'est l'occasion de rappeler que l'ordinateur
ne réfléchit pas. Il traite des nombres sans avoir la moindre possibilité
de comprendre ce que signifient ces nombres.
Quand tu as résolu le problème précédent,
vérifie que tu es capable de déterminer le nombre
de mensualités
si l'on envisage de rembourser 500 par mois pour un
capital de 10 000 .
|
|
| Quand ta feuille de calculs fonctionne correctement pour
tous les cas, passe à l'étape suivante. |
Exercices non commentés
|
Résous les exercices ci-dessous.
|
|
 Pour
connaître le prix TTC d'un article sur lequel le taux de TVA est
de 21%, un commerçant dispose de la feuille de calcul illustrée ci-contre.
Pour des raisons commerciales, il voudrait vendre un article au
prix de 199,90 TTC. A quel prix hors TVA doit-il facturer cet
article?
|
|
 La
cellule B2 d'une feuille de calculs contient une valeur x ;
la cellule C2 contient la valeur de f(x)=3.sin(x)-4.cos²(x)
On demande de déterminer pour quelle valeur de x, la fonction
f(x) a pour valeur 0.
|
|
La cellule B2 d'une feuille de calculs contient une valeur x ;
la cellule C2 contient la valeur de f(x) =  .
On demande de déterminer pour quelle valeur de x, la fonction
f(x) a pour valeurs:
|
|
| Quand tu as résolu les exercices proposés, passe à l'étape suivante. |
Détermination du minimum d'une fonction
|
La technique de recherche d'une valeur cible est puissante.
Cependant, elle est limitée à la recherche d'une valeur unique en
fonction de la valeur d'une cellule unique.
Pour résoudre des problèmes plus complexes, on peut faire appel
à un complément d'Excel appelé Solveur.
|
|
Installer le solveur
Le solveur est un outil additionnel d'Excel. Il n'est pas installé
par défaut. Il faut donc vérifier qu'il est installé avant de pouvoir
l'utiliser.
- Dans le menu Outils, vérifie la présence de la commande Solveur...
Si la commande figure dans le menu, tu peux passer les lignes qui
suivent jusqu'au prochain titre.
- Sélectionne la commande Macros Complémentaires...
- Dans la boîte de dialogue qui apparaît, sélectionne l'option
Solveur et coche la case correspondante.
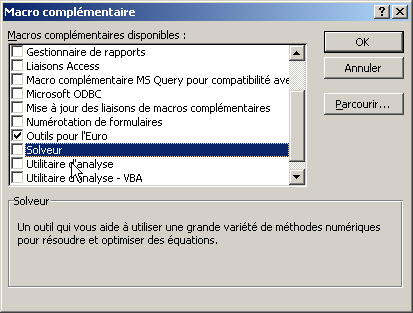
Le solveur est maintenant installé.
Il se pourrait, en fonction de l'installation originale d'Excel,
que le Solveur n'apparaisse pas dans la boîte de dialogue présentée
ci-dessus. Il faut alors procéder à une ré-installation d'Excel à partir
du CD d'installation.
|
|
Recherche du maximum absolu
Nous allons chercher la valeur du maximum de la fonction f(x) =
4.x.(1-x). Commençons par établir une feuille de calculs qui détermine la
valeur de f(x) pour n'importe quelle valeur de x, comme sur l'illustration
ci-dessous.
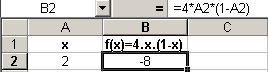
Tout ceci ne demande aucun outil particulier.
- Dans le menu Outils, sélectionne la commande Solveur
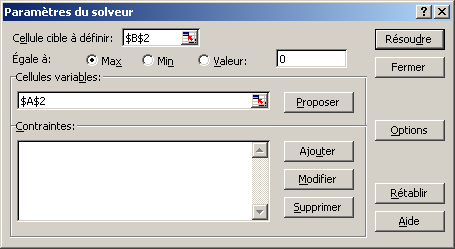
- Dans la zone Cellule cible à définir, sélectionne la cellule
B2
- Parmi les options Egale à, sélectionne Max
- Dans la zone Cellules variables, sélectionne la cellule A2
- Clique sur Résoudre.
Le solveur annonce qu'il a trouvé une solution:
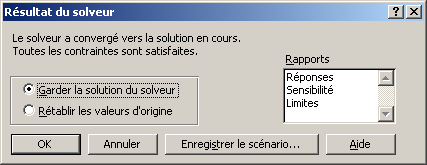
- Clique sur le bouton OK pour garder cette solution.
|
 |
Quelle méthode pourrait-on envisager pour trouver le minimum
de la fonction en utilisant le solveur?
Tente de mettre cette méthode en oeuvre et explique pourquoi elle
ne donne pas de résultat probant.
|
|
| Quand tu as déterminé le maximum de la fonction et réfléchis
à la méthode pour trouver le minimum, passe à l'étape suivante. |
Minimum d'une fonction dans un intervalle
|
A l'étape précédente, nous avons déterminé le minimum
absolu d'une fonction mathématique.
Le solveur permet également de déterminer le minimum d'une fonction
dans un intervalle déterminé.
|
|
- Sur une feuille de calcul vierge, établis quatre cellules
comme sur l'illustration ci-dessous:
Nous allons déterminer le minimum de cette fonction dans
l'intervalle [0 ; -3.14].
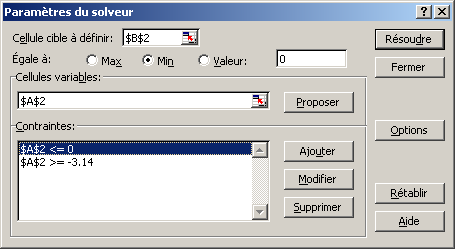
- Dans la zone Cellule cible à définir,
sélectionne la cellule B2
- Parmi les options Egale à, sélectionne Min
- Dans la zone Cellules variables, sélectionne
la cellule A2
- Clique sur le bouton Ajouter de la zone Contraintes
- Définis la première contrainte comme illustré ci-dessous:
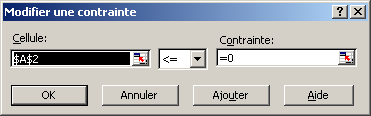
- Clique sur le bouton Ajouter
- Ajoute la deuxième contrainte: la valeur de x > -3,14
(attention, il faut obligatoirement utiliser le '.' et
non la ',' dans cette valeur qui apparaît dans
la contrainte).
- Clique sur le bouton OK
- Clique sur le bouton Résoudre.
|
|
Que se passe-t-il lorsque l'on demande de déterminer le maximum
de la fonction précédente entre -6,28 et +6,28?
Quelle remarque cela impose-t-il?
|
|
| Quand tu as déterminé la valeur du minimum et du maximum
de la fonction dans l'intervalle demandé, passe à l'étape suivante. |
Un peu de pâtisserie avec le solveur
|
La confection d'une tarte
demande d'utiliser: |
La confection de gaufres
demande d'utiliser: |
- 2 oeufs
- 250 grammes de farine
- 0,5 litres de lait
|
- 3 oeufs
- 300 grammes de farine
- 0,7 litres de lait
|
La feuille de calculs illustrée ci-desous devra permettre
de calculer les quantités de farine et de lait lorsque l'on
change le nombre d'oeufs.
Elle calcule également le coût de chaque ingrédient
au tarif suivant:
- oeufs: 0,20/pièce
- farine: 0,50/kg
- lait: 0,60/Litre
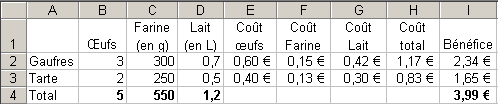
Le bénéfice est calculé en doublant le coût.
|
|
- Reproduit la feuille de calculs de manière à ce qu'elle détermine
les quantités des différents ingrédients pour X gaufres et Y
tartes.
- On dispose de 100 oeufs, 12 kg de farine et 25 litres
de lait. Quelles pâtisseries faut-il produire pour obtenir
le meilleur bénéfice?
Si une première tentative de résolution de l'exercice
fournit des résultats irréalistes, il faut ajouter
les contraintes qui conviennent.
|
|
| Quand tu as déterminé la meilleure façon
de faire des bénéfices pâtissiers, passe à l'étape suivante. |
Kidmobil: l'heure des jeux
|
La société « KidMobil » fabrique
du matériel pour plaines de jeux.
Elle propose, à son catalogue, trois jeux différents
: le modèle « Économique », le modèle « De
Luxe » et le modèle « King Size ». Ces
différents articles sont fabriqués à partir
de pièces détachées qui peuvent servir pour
différents jeux.
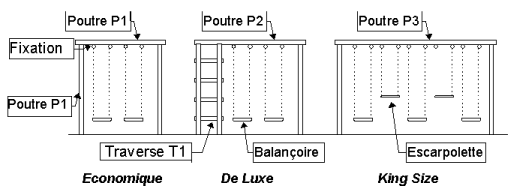
Le tableau 1 ci-dessous indique quelles pièces sont utilisées
pour chacun des jeux ainsi que le nombre ce chaque pièce
nécessaire.
| Modèle |
Poutre P1 |
Poutre P2 |
Poutre P3 |
Traverse T1 |
Balançoire |
Escarpolette |
Fixation |
| Économique |
3 |
0 |
0 |
0 |
2 |
0 |
4 |
| De Luxe |
3 |
1 |
0 |
4 |
2 |
0 |
4 |
| King Size |
2 |
0 |
1 |
0 |
3 |
2 |
10 |
Chaque article dégage une marge bénéficiaire
propre indiquée dans le tableau 2.
| Modèle |
Marge bénéficiaire |
| Économique |
150 |
| De Luxe |
175 |
| King Size |
250 |
Le stock de pièces détachées en magasin est
indiqué dans le tableau 3.
| Pièce |
Stock |
| Poutre P1 |
220 |
| Poutre P2 |
40 |
| Poutre P3 |
30 |
| Traverse T1 |
150 |
| Balançoire |
210 |
| Escarpolette |
50 |
| Fixation |
550 |
On se demande comment utiliser le stock de pièces détachées
disponible afin de dégager le meilleur bénéfice
total après la vente. Pour répondre à cette
question, on établit une feuille de calcul sur le modèle
précisé ci-dessous.
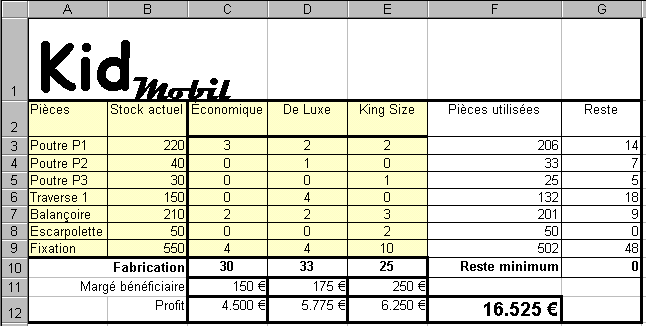
- Les parties grisées du tableau correspondent à des
informations données ;
- la ligne « Fabrication » indique les quantités
de chaque article que l'on envisage de fabriquer ;
- toutes les autres informations sont calculées ;
- la cellule intitulée « Reste minimum » indique
le plus petit nombre d'articles restant en stock après
fabrication. Elle est calculée à l'aide d'une
fonction statistique.
|
|
- Établis la feuille de calcul de manière tout à fait
classique.
- Modifie les valeurs du nombre de pièces fabriquées
pour chaque modèle de manière à pouvoir évaluer
le profit total réalisé dans chacun des cas. Quelle
est la combinaison qui permet d'atteindre le meilleur profit ?
Attention, il ne faut pas utiliser plus d'articles que
le nombre en stock!
- Utilise le solveur afin de déterminer le profit maximum
réalisable. Détermine d'abord quelles sont
les cellules variables et quelles sont les contraintes éventuelles
pour ce problème.
|
|
| Quand tu as déterminé la méthode pour
maximiser le profit de ton entreprise, passe à l'étape suivante. |
Maximisation des intérêts d'un
dépôt en banque
|
Pour le calcul des intérêts composés sur un certain capital, on
peut déterminer, chaque année, le montant des intérêts. Ce montant
est ensuite ajouté au capital.
L'année suivante, on reproduit le calcul avec le capital augmenté
des intérêts. Et ainsi de suite, d'année en année.
|
|
 L'illustration
ci-contre représente l'évolution
de la valeur d'un dépôt en banque à un
taux d'intérêt composé déterminé:
- les cellules B1 et D1 sont variables ;
- les cellules B4 à B14 contiennent des formules qui permettent de déterminer la
valeur du dépôt après chaque année.
- Construis cette feuille de calcul.
- Utilise ensuite le solveur pour déterminer
le taux nécessaire
pour obtenir 17 000 au bout de 10 ans pour un
dépôt
de 10 000 .
En modifiant légèrement la feuille de calcul, il est
possible de faire déterminer le taux nécessaire pour
multiplier le capital de départ par un certain facteur multiplicatif.
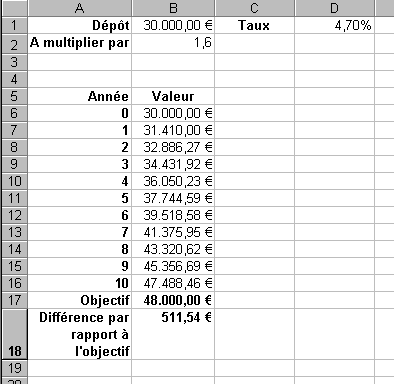
Il suffit alors de vérifier que l'écart par rapport à l'objectif
fixé est nul.
- Établis cette nouvelle feuille de calcul.
- Essaye différentes valeurs de taux (cellule
D1), de manière à atteindre
l'objectif.
- Utilise ensuite le solveur pour déterminer la valeur du
taux à obtenir
pour atteindre l'objectif.
|
|
| Bravo tu as fini !! |
Droits d'auteur : Yves Mairesse. Ce cours est sous
contrat Creative Commons
