Tu dois devenir capable de
 |
Savoir
- expliquer la notion de fonction en informatique ;
- expliquer la notion d'argument d'une fonction.
Savoir faire
- utiliser l'assistant de fonctions de Excel pour établir
des formules contenant des fonctions ;
- établir au clavier des formules contenant des fonctions.
|
|
Les fonctions sur les calculatrices scientifiques
 |
 La
notion de fonction est bien connue des utilisateurs des calculatrices
scientifiques. Il s'agit, schématiquement, d'une
opération mathématique qui, a une valeur d'un
ensemble de départ fait correspondre une autre valeur d'un
autre ensemble. La
notion de fonction est bien connue des utilisateurs des calculatrices
scientifiques. Il s'agit, schématiquement, d'une
opération mathématique qui, a une valeur d'un
ensemble de départ fait correspondre une autre valeur d'un
autre ensemble.
 Exemples:
la fonction « sinus », la fonction « racine
carrée »,
la fonction « carré », ... Exemples:
la fonction « sinus », la fonction « racine
carrée »,
la fonction « carré », ...
Dans le cadre de la fonction y = f(x),
- x est l'argument de la fonction;
- y est le résultat de la fonction.
A l'aide d'une calculatrice, le calcul de y = f(x) se déroule
en trois étapes:
1 |
On introduit la valeur de x
(l'argument de la fonction) au clavier de la calculette |
2 |
On frappe la touche de la fonction:
le calcul est effectué. |
3 |
Le résultat y
est fourni à l'affichage de la calculette |
Les programmes « tableurs » disposent également
d'un certain nombre de fonctions intégrées,
spécialisées dans différents domaines. Dans
ce cadre, les fonctions sont des expressions qui s'utilisent
dans des formules affectées à des cellules.
|
| |
|
|
| Quand tu distingues bien le résultat et l'argument
d'une fonction, passe à l'étape suivante. |
Représentation des fonctions
 |
 Nous pouvons comparer les fonctions à des machines automatiques
qui, lorsqu'on leur fournit une valeur, nous en renvoient une
autre à la place. Les fonctions sont des machines qui servent
à opérer des transformations.
Nous pouvons comparer les fonctions à des machines automatiques
qui, lorsqu'on leur fournit une valeur, nous en renvoient une
autre à la place. Les fonctions sont des machines qui servent
à opérer des transformations. Une fonction demande
généralement qu'on lui fournisse un ou plusieurs
« arguments ».
 Le
ou les arguments sont placés dans le tiroir de la machine
« fonction ». Le tiroir est alors refermé et
la machine utilise la valeur que nous lui avons fournie pour en
calculer une autre : l'image de la valeur. Le
ou les arguments sont placés dans le tiroir de la machine
« fonction ». Le tiroir est alors refermé et
la machine utilise la valeur que nous lui avons fournie pour en
calculer une autre : l'image de la valeur.
 Lorsque
la machine « fonction » a fini d'effectuer son
calcul, elle renvoie une valeur (représentée par un
affichage digital). Lorsque
la machine « fonction » a fini d'effectuer son
calcul, elle renvoie une valeur (représentée par un
affichage digital).
Les valeurs fournies à une fonction sont appelées
« arguments » de la fonction.
En informatique, une fonction peut demander zéro, un ou
plusieurs arguments.
|
 |
|
| |
|
|
| Quand tu as répondu aux questions et bien compris les
réponses, passe à l'étape suivante. |
Calcul de la moyenne d'une liste de valeurs
 |
 Un
étudiant souhaite pouvoir calculer automatiquement la moyenne
de ses résultats d'évaluations en différentes
branches. Il établit pour cela une feuille de calcul du type
illustré ci-contre. Un
étudiant souhaite pouvoir calculer automatiquement la moyenne
de ses résultats d'évaluations en différentes
branches. Il établit pour cela une feuille de calcul du type
illustré ci-contre.
La moyenne doit être indiquée dans la cellule B6.
|
 |
- Si ce n'est déjà fait, sélectionne la cellule
B6 dans laquelle doit apparaître le résultat du calcul.
 Clique
sur le bouton Clique
sur le bouton  de la barre de formules, afin de signaler que tu vas indiquer
un calcul. Effectivement, tous les calculs sont reconnaissables
au signe = qui les introduit.
de la barre de formules, afin de signaler que tu vas indiquer
un calcul. Effectivement, tous les calculs sont reconnaissables
au signe = qui les introduit.
La liste des fonctions directement disponibles s'ouvre à
gauche de la barre de formules. |
| |
 Si
la fonction Moyenne n'apparaît pas immédiatement
dans la partie gauche de la barre de formules, sélectionne-la
dans la liste déroulant disponible en cliquant sur la flèche
vers le bas (voir les illustrations ci-dessus et à droite). Si
la fonction Moyenne n'apparaît pas immédiatement
dans la partie gauche de la barre de formules, sélectionne-la
dans la liste déroulant disponible en cliquant sur la flèche
vers le bas (voir les illustrations ci-dessus et à droite). |
|
Une nouvelle boîte de dialogue apparaît.
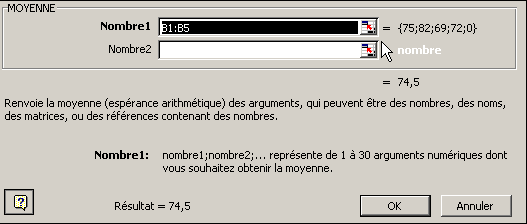
Dans la partie supérieure de la boîte
de dialogue, et entouré d'un cadre, apparaît la liste
des arguments de la fonction. Cette liste est actuellement composée
de deux lignes.
Après avoir examiné les cellules voisines
de B6, Excel propose que la moyenne soit calculée
sur l'ensemble des cellules B1:B5. Malheureusement, son
estimation n'est pas tout à fait correcte puisque la cellule
B5 ne doit pas être utilisée dans le calcul.
Dans la partie inférieure, une explication
succincte de la fonction Moyenne permet de mieux comprendre
la façon de l'utiliser.
Finalement, Excel indique le résultat de la
fonction, sur la base des arguments actuellement fournis.
|
 |
 Clique
sur le bouton Clique
sur le bouton  à droite du premier argument de la fonction.
à droite du premier argument de la fonction.- Par un cliquer/glisser, sélectionne la zone qui contient
les nombres à introduire dans le calcul: B1:B4
L'indication de la zone B1:B4 apparaît sous le nom
de la fonction Moyenne.
- Lâche le bouton de la souris.
- Clique sur le bouton
 afin de retourner à la boîte de dialogue précédente.
afin de retourner à la boîte de dialogue précédente.
|
|
 En
fait, tu n'as qu'un seul argument à fournir à la fonction
Moyenne: la liste des valeurs à prendre en compte
dans le calcul. En
fait, tu n'as qu'un seul argument à fournir à la fonction
Moyenne: la liste des valeurs à prendre en compte
dans le calcul.
La formule finale apparaît dans la barre de formules et le
résultat est indiqué en B6.
- Modifie quelques valeurs des notes des différents cours
afin de confirmer que la moyenne est correctement calculée.
- Supprime l'une des notes. Constate ce qui se produit.
|
|
La syntaxe pour l'usage d'une fonction est donc:
- un signe = pour annoncer un calcul
- le nom de la fonction
- suivi de parenthèses
- contenant le ou les arguments de la fonction.
|
| |
|
|
| Quand tu as compris le fonctionnement de la fonction Moyenne,
passe à l'étape suivante. |
Calcul d'une moyenne avec plusieurs arguments
|
Heureux du résultat obtenu pour le calcul
de sa cote moyenne pour une période de l'année, l'élève
évoqué à l'étape précédente souhaite
pouvoir utiliser sa feuille de calcul pour l'ensemble des trois
périodes de l'année scolaire.
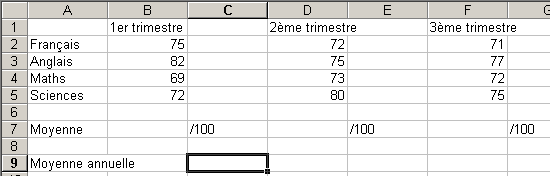
Il établit donc une feuille sur le modèle ci-dessus.
|
 |
Celle-ci peut être téléchargée en
suivant la procédure suivante:
- un clic droit sur l'illustration,
- choisis la commande 'Enregistrer la cible sous'
- indique ton répertoire personnel pour l'enregistrement
- ouvre ce document avec Excel.
|
 |
- Dans les cellules B7, D7 et F7, calcule
la moyenne de chaque trimestre.
Dans la cellule C9, tu vas calculer la moyenne générale
des trois trimestres.
- Clique sur le bouton
 à gauche de la barre de formules
à gauche de la barre de formules
- Sélectionne la fonction Moyenne
- Clique sur le bouton
 à droite de la zone correspondant au premier argument
à droite de la zone correspondant au premier argument
- Sélectionne la cellule B7 puis clique sur le bouton
 pour retourner à la boîte de dialogue
pour retourner à la boîte de dialogue
- Clique sur le bouton
 à droite de la zone correspondant au deuxième argument
à droite de la zone correspondant au deuxième argument
- Sélectionne la cellule D7 puis clique sur le
bouton
 pour
retourner à la boîte de dialogue pour
retourner à la boîte de dialogue
Dans la boîte de dialogue, une nouvelle ligne est apparue
pour un troisième argument. En fait, la boîte de dialogue
peut accueillir jusqu'à 30 arguments, comme indiqué
dans les explications qui y sont fournies.
- Clique sur le bouton
 à droite de la zone correspondant au troisième argument
à droite de la zone correspondant au troisième argument
- Sélectionne la cellule F7 puis clique sur le
bouton
 pour
retourner à la boîte de dialogue pour
retourner à la boîte de dialogue
- Clique sur le bouton OK.
La moyenne générale est calculée.
Compare la formule notée dans la barre de
formules pour la cellule C9 et pour les cellules B7,
D7 et F7.
|
|
Dans la cellule B7, par exemple, la formule indiquée
doit être =MOYENNE(B2:B6).
Le double point ' : ' sépare les deux
limites de la zone de cellules sur lesquelles il faut calculer
la moyenne.
Dans la cellule C9, la formule indiqué doit être =MOYENNE(B7;D7;F7).
Les ' ; ' séparent les différents
arguments de la fonction.
|
|
La syntaxe pour l'usage d'une fonction est donc:
- un signe = pour annoncer un calcul
- le nom de la fonction
- suivi de parenthèses
- contenant le ou les arguments de la fonction séparés
par le symbole ' ; '.
|
| |
|
|
| Quand tu as compris le fonctionnement de la fonction Moyenne
avec plusieurs arguments, passe à l'étape suivante. |
Une fonction sans argument... et d'autres
 |
Excel permet l'utilisation de certaines fonctions
sans arguments. C'est le cas de la fonction qui retourne la valeur
de Pi (3,14159).
Tu vas, dans la foulée, apprendre à insérer
une fonction selon une autre méthode.
|
 |
 Ouvre
une nouvelle feuille de calcul Ouvre
une nouvelle feuille de calcul- Dans cette feuille, reporte les indications fournies dans l'illustration
ci-contre.
|
| |
|
| |
 Dans
la cellule B2, tu vas indiquer la valeur de Pi/3. Dans
la cellule B2, tu vas indiquer la valeur de Pi/3.
- Sélectionne la cellule B2.
- Clique sur le bouton
 de la barre d'outils standard d'Excel.
de la barre d'outils standard d'Excel.
- Dans la boîte de dialogue qui apparaît, sélectionne
- Math et Trigo dans la liste Catégorie de fonctions
- Pi dans la liste Nom de la fonction
- Clique le bouton OK.
|
| |
La fonction est collée automatiquement dans la barre de
formules.
La boîte de dialogue classique apparaît, mais elle
ne contient aucune zone pour des arguments.
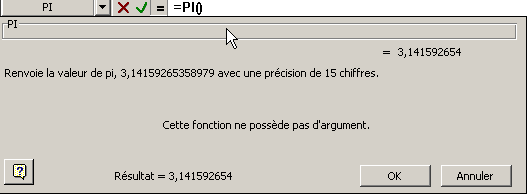
La fonction Pi est sans argument. Elle s'écrit donc simplement
=PI().
|
 |
- Dans la barre de formules, termine de noter =PI()/3.

La valeur de Pi/3 apparaît dans la cellule B2.
- En utilisant l'une ou l'autre méthode d'écriture
de formule, complète la colonne B du tableau avec les valeurs
de Pi/2, Pi, 2xPi/3,...
Remarque: les fonctions peuvent également être indiquées
'manuellement'. Si tu écris =Pi() dans une cellule,
Excel 'comprend' qu'il s'agit bien de la fonction Pi.
|
 |
 Termine
maintenant le travail en complétant les colonnes C et D. Termine
maintenant le travail en complétant les colonnes C et D.
Tu trouveras les fonctions Sinus et Cosinus dans la catégorie
Math et Trigo.
Quand le travail est terminé, le tableau se présente
comme sur l'illustration ci-contre.
 Ouh laaaaa! Mais
c'est quoi ça? Il n'est pas en forme, Excel, ou bien? C'est
plutôt bizarroïde ce 6,125E-17. Kézako? Ouh laaaaa! Mais
c'est quoi ça? Il n'est pas en forme, Excel, ou bien? C'est
plutôt bizarroïde ce 6,125E-17. Kézako?
 Etonnant, mais
pas très difficile à comprendre. Excel utilise ici
la notation scientifique. Ce qu'il écrit 6,125E-17 se lit
'6,125 fois dix exposant -17' ou encore 0,00000000000000006125.
C'est aussi simple que ça. Etonnant, mais
pas très difficile à comprendre. Excel utilise ici
la notation scientifique. Ce qu'il écrit 6,125E-17 se lit
'6,125 fois dix exposant -17' ou encore 0,00000000000000006125.
C'est aussi simple que ça.
 Hé, mais
ça ne va pas du tout, ça!! Le cosinus de Pi/2, c'est
0: tout le monde sait ça! Il nous fait de la fièvre,
là, ce tableur? Hé, mais
ça ne va pas du tout, ça!! Le cosinus de Pi/2, c'est
0: tout le monde sait ça! Il nous fait de la fièvre,
là, ce tableur?
 Ta surprise
est tout à fait compréhensible. Effectivement, Excel
commet ici plusieurs erreurs. Remarque également la valeur
du sinus de Pi. Ta surprise
est tout à fait compréhensible. Effectivement, Excel
commet ici plusieurs erreurs. Remarque également la valeur
du sinus de Pi.
En fait, ces 'erreurs' sont liées à la façon
dont le logiciel calcule les fonctions trigonométriques:
ses méthodes contiennent des approximations. De ce fait,
le cosinus de Pi/2 est 'presque' = 0, mais pas tout à
fait.
Dans la plupart des cas, il nous suffira de nous souvenir que les
valeurs calculées sont approximatives. Les 'erreurs'
commises sont généralement négligeables.
|
| |
|
|
| Quand tu as terminé de compléter le tableau,
passe à l'étape suivante. |
Exercice d'application 1
 |
Télécharge la feuille de calcul ' mobilier.xls '
et enregistre-la dans ton répertoire personnel.
Cette feuille présente les résultats des ventes d'un
magasin de meuble pour une période donnée. Le gérant
souhaite pouvoir obtenir des informations sur les résultats
financiers correspondant à cette période, sur la base
des informations fournies par les vendeurs.
Examine quelques instants la feuille de calcul puis réalise
les opérations indiquées ci-dessous. Certaines demanderont
d'utiliser des fonctions, d'autres pas.
Quand c'est nécessaire, cherche dans l'ensemble des fonctions
disponibles celles qui pourraient t'être utiles.
|
 |
Les cellules encadrées en rouge doivent recevoir les formules
qui conviennent, selon les indications données ci-dessous.
- Dans les cellules B20 et C20, calcule la somme
des valeurs indiquées dans la colonne.
- Dans les cellules D5:D19, calcule les montants de la
marge bénéficiaire sur chaque article. La marge
bénéficiaire est la différence entre le prix
de vente et le prix d'achat.
- Dans les cellules F5:F19, calcule le montant des bénéfices
réalisés sur l'ensemble des ventes de chaque article.
Ce montant s'obtient en multipliant la marge bénéficiaire
par le nombre d'articles vendus.
- Dans la cellule F20, calcule le bénéfice
total pour la période.
- Dans la cellule B22, calcule le nombre total d'articles
vendus.
- Dans la cellule B23, calcule la marge bénéficiaire
moyenne.
- Dans les cellules B24 et B25, calcule les
meilleur et moins bon bénéfices.
- Dans la cellule B28, fait calculer la date du jour
(vois les fonctions Date & Heure).
|
| |
|
|
| Quand ta feuille de calcul est complétée et
enregistrée, et passe à
l'étape suivante. |
Exercice d'application 2
 |
Télécharge la feuille de calcul ' amortis.xls '
et enregistre-la dans ton répertoire personnel.
La société « Duschtroumpf and Co » spécialisée
dans le transport de marchandises vient d'acheter un camion
de valeur 62500 . On suppose que la valeur de revente
du véhicule diminue de 30% à chaque année qui
passe.
En utilisant la fonction d'amortissement linéaire
(AMORLIN), on demande de déterminer la valeur de
l'amortissement en fonction du nombre d'années
de service du camion et de la valeur de revente espérée.
Sois attentive-attentif à l'utilisation correcte des références
relatives et absolues.
|
 |
Les cellules encadrées en rouge doivent recevoir les formules
qui conviennent, selon les indications données ci-dessous.
- Dans la cellule B5, calcule le prix résiduel
du camion après un an.
- Dans la cellule B6, calcule le prix résiduel
du camion après la deuxième année.
- Recopie la formule de B6 dans la zone B7:B10.
- Dans la cellule D5, calcule l'amortissement pour la
première année.
- Recopie la formule de D5 dans la zone D6:D10.
Le résultat attendu est du type suivant:
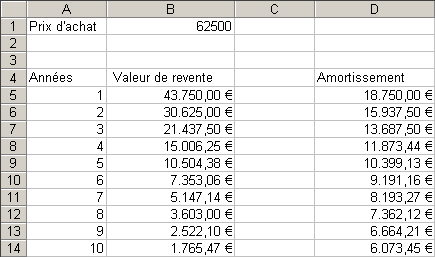
|
| |
|
|
| Quand ta feuille de calcul est complétée et
enregistrée, passe à
l'étape suivante. |
Exercice d'application: décroissance radioactive
|
Application 'défi' pour les as du PC et des maths... Oseras-tu?
|
|
Une substance radioactive contient des atomes instables
qui ont tendance à se désintégrer.
Ainsi, le 14C se désintègre
spontanément selon le schéma suivant:
14C  14N + e- 14N + e-
 A
tout instant, chaque atome 14C a une
certaine probabilité (assez faible) de se désintégrer. A
tout instant, chaque atome 14C a une
certaine probabilité (assez faible) de se désintégrer.
Si l'on considère un grand échantillon d'atomes 14C
(1 mol, par exemple), cet échantillon se transforme petit
à petit en 14N.
Au bout de 5730 années (une période), environ, la
masse de 14C est divisée en
deux.
Si l'on attend 5730 nouvelles années, la masse de l'échantillon
précédent se trouve à nouveau divisée
par deux.
C'est ce qui est illustré dans le tableau ci-contre. Plus
le temps passe, moins la radioactivité de l'échantillon
est importante: c'est la décroissance radioactive.
|
 |
 Reproduis
le tableau présenté ci-dessus. Il doit être
possible de choisir n'importe quelle quantité de 14C
dans la cellule B2. Toutes les autres valeurs s'ajustent automatiquement.
Aucune fonction d'Excel n'est nécessaire ici. Reproduis
le tableau présenté ci-dessus. Il doit être
possible de choisir n'importe quelle quantité de 14C
dans la cellule B2. Toutes les autres valeurs s'ajustent automatiquement.
Aucune fonction d'Excel n'est nécessaire ici.- Etablis le diagramme de la population d'atomes 14C
en fonction du temps.
- Introduis la courbe de tendance en choisissant le type 'exponentielles'.
- Demande à voir l'équation de la courbe sur le
graphique.
Cette équation pourrait s'écrire sous la forme:
Pt = p0.e-k.t
où k est appelée ' constante
de radioactivité '.
- Sur une nouvelle feuille de calcul, établis la courbe
de décroissance radioactive du 14C
en utilisant la fonction exponentielle d'Excel.
La valeur de k donnée par Excel est assez approximative.
Tente, par essais successifs, de trouver la valeur de k pour obtenir
une période aussi proche que possible de 5730 années.
- L'élément 131I est
caractérisé par une période de 8,04 jours.
Trace le diagramme de décroissance radioactive. Tente,
par essais successifs, de déterminer la valeur de k pour
cet élément.
|
| |
|
|
| Quand ta feuille de calcul est complétée et
enregistrée, passe à
l'étape suivante. |
Exercice d'application: un jeu de dés
|
Parmi les fonctions disponibles dans Excel, nous
disposons de tout ce qui est nécessaire pour programmer un
jeu de dés palpitant.
La fonction =alea() est un peu particulière: elle ne demande
aucun argument et renvoie une valeur, au hasard, comprise dans l'intervalle
[0 ; 1[.
Une autre fonction nous sera encore utile: la fonction =ent() demande
un seul argument dont elle retourne la partie entière.
|
 |
- Ouvre une nouvelle feuille de calcul.
- Dans la cellule A1, indique la formule =alea(). Frappe la touche
F9 (qui force le recalcul de l'ensemble de la feuille).
- Dans la cellule A2, indique la formule =alea()*10. Frappe la
touche F9. Observe le résultat.
En utilisant les informations données ci-dessus, imagine
maintenant quelle formule devrait être introduite dans la
cellule A1 pour simuler un lancer de dé.
 Simule
un jeu avec 3 dés indépendants. La feuille de calcul
détermine, de plus, la somme des points obtenus pour le lancer. Simule
un jeu avec 3 dés indépendants. La feuille de calcul
détermine, de plus, la somme des points obtenus pour le lancer.
Ajoute 3 dés pour un adversaire ; la somme est également
calculée.
Tu es autorisé(e) à jouer quelques instants contre
ton voisin le plus immédiat dans la salle de cours. Tu as
les bleus, ton adversaire à les jaunes. Bonne chance!!
|
| |
|
|
| Quand le jeu est au point,
sache que tu as fini !! |
Droits d'auteur : Yves Mairesse. Ce cours est sous
contrat Creative Commons



 La
notion de fonction est bien connue des utilisateurs des calculatrices
scientifiques. Il s'agit, schématiquement, d'une
opération mathématique qui, a une valeur d'un
ensemble de départ fait correspondre une autre valeur d'un
autre ensemble.
La
notion de fonction est bien connue des utilisateurs des calculatrices
scientifiques. Il s'agit, schématiquement, d'une
opération mathématique qui, a une valeur d'un
ensemble de départ fait correspondre une autre valeur d'un
autre ensemble. Exemples:
la fonction « sinus », la fonction « racine
carrée »,
la fonction « carré », ...
Exemples:
la fonction « sinus », la fonction « racine
carrée »,
la fonction « carré », ... Nous pouvons comparer les fonctions à des machines automatiques
qui, lorsqu'on leur fournit une valeur, nous en renvoient une
autre à la place. Les fonctions sont des machines qui servent
à opérer des transformations.
Nous pouvons comparer les fonctions à des machines automatiques
qui, lorsqu'on leur fournit une valeur, nous en renvoient une
autre à la place. Les fonctions sont des machines qui servent
à opérer des transformations.  Le
ou les arguments sont placés dans le tiroir de la machine
« fonction ». Le tiroir est alors refermé et
la machine utilise la valeur que nous lui avons fournie pour en
calculer une autre : l'image de la valeur.
Le
ou les arguments sont placés dans le tiroir de la machine
« fonction ». Le tiroir est alors refermé et
la machine utilise la valeur que nous lui avons fournie pour en
calculer une autre : l'image de la valeur. Lorsque
la machine « fonction » a fini d'effectuer son
calcul, elle renvoie une valeur (représentée par un
affichage digital).
Lorsque
la machine « fonction » a fini d'effectuer son
calcul, elle renvoie une valeur (représentée par un
affichage digital). Un
étudiant souhaite pouvoir calculer automatiquement la moyenne
de ses résultats d'évaluations en différentes
branches. Il établit pour cela une feuille de calcul du type
illustré ci-contre.
Un
étudiant souhaite pouvoir calculer automatiquement la moyenne
de ses résultats d'évaluations en différentes
branches. Il établit pour cela une feuille de calcul du type
illustré ci-contre. Clique
sur le bouton
Clique
sur le bouton  Si
la fonction Moyenne n'apparaît pas immédiatement
dans la partie gauche de la barre de formules, sélectionne-la
dans la liste déroulant disponible en cliquant sur la flèche
vers le bas (voir les illustrations ci-dessus et à droite).
Si
la fonction Moyenne n'apparaît pas immédiatement
dans la partie gauche de la barre de formules, sélectionne-la
dans la liste déroulant disponible en cliquant sur la flèche
vers le bas (voir les illustrations ci-dessus et à droite).
 Clique
sur le bouton
Clique
sur le bouton  En
fait, tu n'as qu'un seul argument à fournir à la fonction
Moyenne: la liste des valeurs à prendre en compte
dans le calcul.
En
fait, tu n'as qu'un seul argument à fournir à la fonction
Moyenne: la liste des valeurs à prendre en compte
dans le calcul.
 Ouvre
une nouvelle feuille de calcul
Ouvre
une nouvelle feuille de calcul Dans
la cellule B2, tu vas indiquer la valeur de Pi/3.
Dans
la cellule B2, tu vas indiquer la valeur de Pi/3.

 Termine
maintenant le travail en complétant les colonnes C et D.
Termine
maintenant le travail en complétant les colonnes C et D. Ouh laaaaa! Mais
c'est quoi ça? Il n'est pas en forme, Excel, ou bien? C'est
plutôt bizarroïde ce 6,125E-17. Kézako?
Ouh laaaaa! Mais
c'est quoi ça? Il n'est pas en forme, Excel, ou bien? C'est
plutôt bizarroïde ce 6,125E-17. Kézako? Etonnant, mais
pas très difficile à comprendre. Excel utilise ici
la notation scientifique. Ce qu'il écrit 6,125E-17 se lit
'6,125 fois dix exposant -17' ou encore 0,00000000000000006125.
C'est aussi simple que ça.
Etonnant, mais
pas très difficile à comprendre. Excel utilise ici
la notation scientifique. Ce qu'il écrit 6,125E-17 se lit
'6,125 fois dix exposant -17' ou encore 0,00000000000000006125.
C'est aussi simple que ça.
 A
tout instant, chaque atome
A
tout instant, chaque atome  Reproduis
le tableau présenté ci-dessus. Il doit être
possible de choisir n'importe quelle quantité de
Reproduis
le tableau présenté ci-dessus. Il doit être
possible de choisir n'importe quelle quantité de  Simule
un jeu avec 3 dés indépendants. La feuille de calcul
détermine, de plus, la somme des points obtenus pour le lancer.
Simule
un jeu avec 3 dés indépendants. La feuille de calcul
détermine, de plus, la somme des points obtenus pour le lancer.